転がり抵抗を比較 23Cと25Cのタイヤは違うのか？

ツール・ド・フランスなどワールドツアーを転戦するほとんどのプロチームが、25Cのタイヤを選択している。今までのプロツアー機材でレース用のタイヤ幅といえば23Cが主流であった。しかし近年リム幅が広がるのと合わせるようにタイヤの太さも25Cへとシフトしてきている。

太いタイヤのイメージといえば、人間が感じる科学的根拠のない「細いタイヤ＝抵抗が小さい」という事が浸透していまいか。しかし現実には、ツアー・オブ・ドバイにおいて、ほぼすべてのチームのタイヤ幅が23Cより太い25Cを使用しているのだ。

その理由は何なのだろうか。

今回は、平成21年1月26日に行われた経済産業省主管でJATMA(日本自動車タイヤ協会）が行った「低燃費タイヤ等普及促進協議会」の資料と、SCHWALBEの技術資料、そしてGOKISOの資料から、なぜ今「ワールドツアーで２５ｃが主流」なのかを考察する。

なお、JATMA(日本自動車タイヤ協会）は次のの組織から構成されている。
ブリジストン、ミシュラン、ダンロップ、YOKOHAMA、TOYO TIRES。

なぜ太いタイヤを使うのか？

25Cが最近表立って使用されているその理由は、「23Cよりも同一空気圧なら転がり抵抗が少ない」事が理由とされている。トニー・マルティンが世界選手権エリートタイムトライアルで連覇した時も、S-WORKS TURBO 24Cのクリンチャーを使っていた。

ただ単に「トニー・マルティンが速い」という言い方もできるが、写真のように「供給を受けていない他社ロゴを消してまで」使いたいチェーンリングを使うのだから、タイヤ幅24Cを選択した理由もあるのだろう。

ではなぜ太いほうが良いのだろうか。まことしやかに広まっている「良くわからないけど、太いタイヤの方がころがり抵抗が少ない論」を払拭する為、エビデンスを見て行くことにする。詰まるところ、”私も”クリンチャーを全て25Cにすることにした。

転がり抵抗の９割はタイヤの変形

タイヤが転がる際に「転がり抵抗」と呼ばれる抵抗がある。転がることにより、タイヤに発生する抵抗である。その抵抗の原因は何なのか。例えば体感できる「転がり抵抗」の形として自転車（ママチャリ）の空気圧が抜けた状態を想像して欲しい。

空気が抜け、潰れたタイヤで走ると乗り心地も違うし進みにくいといったように、体感して転がりが違うことがわかる。空気が抜けたタイヤは「転がり抵抗」が大きくなり「ペダルが重たくなる」や「進みにくい」といったことが体感できる。

もう少し厳密に考えると、進行方向に対して進みにくくなる事と同じ意味である。すなわち転がり抵抗とは、「進行方向に対して逆向きの抵抗力」といえる。自転車を進ませる上で先般の「自転車を早く進ませる為に考えるべき要素は何か」で紹介したように様々な「抵抗」の種類がある。

空気抵抗もその一部だが、転がり抵抗の要素を決めているのはなにか。タイヤに受ける抵抗は主に３種類に分けられる。

• タイヤ変形
• 接地摩擦
• 空気抵抗

の要因３つである。この３つの中で「転がり抵抗の９０％」を締めている要素がある。それはタイヤ変形だ。では、何が転がり「抵抗」を及ぼしているのかというと、タイヤが変形する事によるエネルギーロスが影響している（先ほどのママチャリの話）。

参考：経済産業省　低燃費タイヤ等普及促進協議会
　　　「資料3：タイヤが自動車燃費に与える影響について」

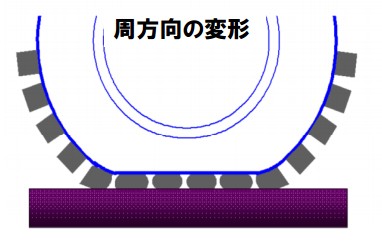
ではどのような変形した場合、タイヤの形状が「転がり抵抗　＝　エネルギーロス」を及ぼしているのか。まずは、タイヤを横から見た時を想像してほしい。タイヤは何も負荷がかかっていない状態であれば真円である。しかし空気を入れ、人間が乗ると負荷がかかる。

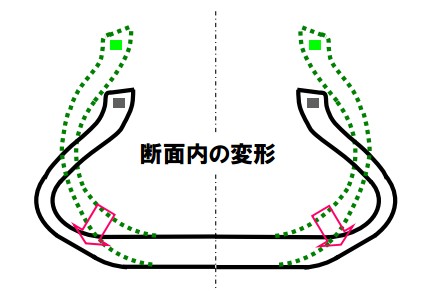
その重みでタイヤは空気圧との兼ね合いで形状が変わる。「横から見た」場合は地面との接地面が平らになる。次は断面図を確認する。同じように何も負荷をかけないと元の形状であるが、負荷をかけると潰れたように変形する。これはイメージがつきやすい。

この「横から見た変形」と「断面から見た変形」の2つの要素がタイヤの転がり抵抗を決めている。これらを弾性損失という。したがってこの「変形」が少なければ少ないほど、弾性損失によるエネルギーロスが小さくなるので「転がり抵抗が小さい」と言える。

ではなぜ、25Cと23Cであれば25Cのタイヤの方が、転がり抵抗が少ないとされているのか。次はSCHWALBEのページにそのヒントが有る。

SCHWALBEの転がり抵抗の技術資料

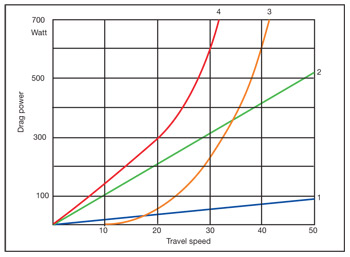
SCHWALBEの技術資料は非常にわかりやすい。結局は先程の経済産業省主管でJATMA(日本自動車タイヤ協会）が行った「低燃費タイヤ等普及促進協議会」の資料と同様の内容になるが、より「自転車」に偏ったな話だ。こちらのほうが面白い。まずは自転車が走ることによる転がり抵抗とその要素を画像で示している。

• 青１．転がり抵抗
• 緑２．勾配５％と仮定した抵抗
• 橙３．空気抵抗
• 赤４．１～３の要素の総合抵抗

まずは青１の転がり抵抗はライダーの体重に左右され、速度が上がるごとに抵抗が増していることになる。空気抵抗も先般の記事の通り、速度の自乗に比例して空気抵抗が増えていく。加速すれば加速するほど、自転車は「あらゆる抵抗」を受けてしまう事を意味している。

当然これらの抵抗の他にも、機材由来のフリクションロス（摩擦抵抗）などがある。

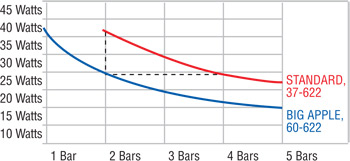
太いタイヤと細いタイヤ同じ空気圧であれば、どちらが抵抗が少ないのか。徐々に革新に迫ってきている。SCHWALBEの技術資料にもある通り（データーとしては極端な例であるが、例としてわかりやすい）太さと空気圧で抵抗値（ワット）が変動している。

このデーターからわかることは、先ほどの経済産業省の「資料3：タイヤが自動車燃費に与える影響について」の説明にも有る通り、弾性損失によるエネルギーロスが小さくなる「閾値」が出現する。上記データーの傾向をまとめると「転がり抵抗が小さい」といえるのは、

• 2Bars:(37c 40Watts, 60c 27.5Watts)
• 3Bars:(37c 32.5Watts, 60c 22.5Watts)
• 4Bars:(37c 27.0Watts, 60c 18.5Watts)
• 5Bars:(37c 24.0Watts, 60c 17.5Watts)

上記の通り同じ空気圧なら「太いほうが転がり抵抗が小さい」というデーターが見て取れる。しかし単純にそう考えてはいけない。例えば同じ27.5Wattsの「転がり抵抗」を考えると、

60c x 2Bars = 37c x 4Barsとなり、「2bar空気を入れた60mm幅のタイヤ」と「4bar空気を入れた37mm幅のタイヤ」の「転がり抵抗」は互いに27.5Wattsであり、転がり抵抗の差はない、ということになる。

すなわち、シクロクロスのように「幅広タイヤと低空気圧」というシチュエーションも考えられるし、ロードのように「細いタイヤと高空気圧」という場合も考えられるのでそれぞれ最適解が異なる。

よって、重要なのはタイヤの太さの特性上どこで「最適解が拮抗」するのかを知ることである。その上でデーター上は「ある空気圧」において、23Cよりも25Cの方が「弾性損失」が少なく「転がり抵抗が小さい」と判断されてもなんらおかしくない。空気圧の適正算出方程式は後ほど説明する。

参考資料：SCHWALBE “Why do wide tires roll better than narrow ones?”

GOKISOの転がり抵抗の説明資料

GOKISOの技術資料にもワイドタイヤの方が抵抗が少ない説明がされている。その前にサイクルスポーツ紙の2009年9月号「タイヤのセッティングで走りを変える」で非常に良い「タイヤ接地面の図」があるので参考にされたい。

参考：サイクルスポーツ 2009年9月号：

上記URLでわかるタイヤの太さと接地面の形状は、タイヤが太くなろうが、細くなろうが同じ空気圧、同じ負荷重量であればさほど「接地面積」はあまり変わらないことがわかる。接地面積が変わらないということは、冒頭の「タイヤを横から見た」際の変形が、細いタイヤの方が大きくなることを意味している。

話は戻りGOKISOの技術説明が一番わかり易いので紹介する。こちらもつまるところ話の内容は「変形量が小さい」＝「ころがり抵抗が小さい」話になる。内容は先ほどの経済産業省の「資料3：タイヤが自動車燃費に与える影響について」の説明にも有る通りだ。

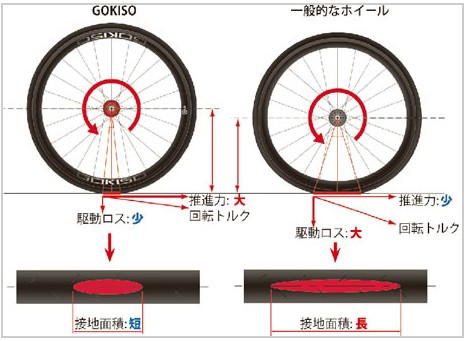
まずはGOKISOもころがり抵抗と駆動抵抗を最小化するためには「接地面積」が関連していると述べている。この内容はSCHWALBEや経済産業省のデーターからも同様にわかる。重複してしまうが、GOKISOの技術資料も同様のことを述べている。

GOKISO技術資料より：http://www.gokiso.jp/products/wheel.html#features

接地面積は”ナロー（細い）”と”ワイド（太い）”は同様である。しかし、先ほどの「タイヤを横から見た弾性変形」はナローのほうが長く狭い（横から見ると潰れている）。

GOKISO技術資料より：http://www.gokiso.jp/products/wheel.html#features

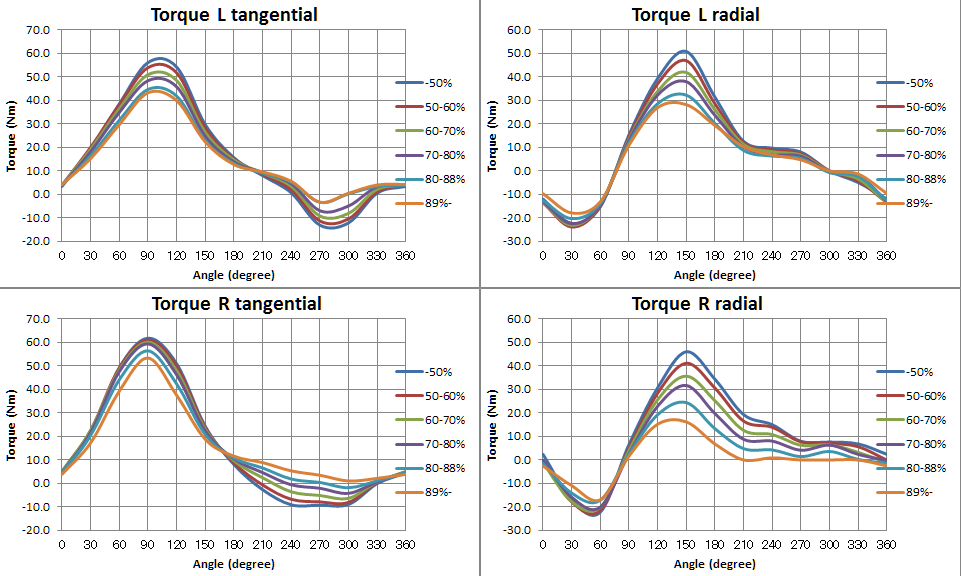
そして非常にGOKISOの技術資料がわかりやすいのは、駆動ロスと推進力の関係である。この回転トルクを見て何かを思い出さないだろうか。そう、「ペダリング効率」である。そのなかで回転に寄与しない「法線方向」の力と回転に寄与する「接線方向」の力があった。

まさにその話と近い（物理的な内容は異なるが）説明がされている。この推進力になっている話は、冒頭にも説明した、進行方向に対して進みにくくなること、すなわち転がり抵抗とは「進行方向に対して逆向きの抵抗力」といえる話がここでも同じように説明されている。

各社25cタイヤ実重量

• GP4000SII 25C 217g, 219g
• Panaracer RACE A 25C 245g
• MAVIC 125 F198g, R188g (リアのほうが軽いです)
• S-WORKS TOURBO 24C 190g, 192g
• MAXXIS 25C テストタイヤ 211g

各社25cタイヤ一覧

現在23c以上のタイヤラインナップをしているメーカーを集めたので、いづれ訪れるであろう25c時代の為にまとめておこう。

Continental

• TU Force comp 28″x24mm
• TU Competition 28″x25mm
• TU Sprinter Gatorskin 28″x25mm
• CL Grand Prix Force 700x24C
• CL Grand Prix 4000 S 700x25C
• CL Grand Prix 4000 700x25C
• CL Grand Prix 4-Season 700x25C
• CL Grand Prix 4-Season 700x28C
• CL Grand Prix GT 700x25C
• CL Grand Prix 700 x 24C
• CL Grand Prix 700 x 28C
• CL Grand Prix Classic 700x25C
• CL Gator Hardshell 700 x 25C
• CL Gator Hardshell 700 x 28C
• CL Gator Hardshell 700 x 32C
• CL Gatorskin 700 x 25C
• CL Gatorskin 700 x 28C
• CL Gatorskin 700 x 32C
• CL Ultra Race 700 x 25C
• CL Ultra Sport 700 x 25C
• CL Ultra Sport 700 x 28C

Vittoria

• TU & CL Corsa CX 700 x 25C
• TU & CL Corsa SC 700 x 25C
• TU & CL Corsa SL 700 x 24C
• TU & CL Corsa SR 700 x 24C
• TU & CL Pave CG 700 x 25C,27C
• TU Crono CS 700 x 24C

MICHELIN

• TU PRO4TU SC 700 x 25C
• CL PRO4SC 700 x 25C
• CL PRO4Endurance 700 x 25C
• CL LITHION 700 x 25C
• CL Dynamic SPORT 700 x 25C

SCHWALBE

• TU & CL ONE 700 x 25C,26C
• CL アルトレモ 700 x 25C

SPECIALIZED

• TU & CL TURBO 24

Panaracer

• CL RACE A 700 x 25C
• CL RACE D 700 x 25C
• TU RACE C 700 x 26C

上記の通り各社から25c以上のタイヤがラインナップされている。この中でコンパウンドの関係から弾性変形の違いが有り全て同じ転がり抵抗と言えない事は抑えておいてほしい。

空気圧の計算方法

空気圧は体重（装備）＋車重で変わる。一般的な最適解を求める計算式を紹介する。

• 20C: 空気圧(psi) = (0.33 * 2.2 * 体重(kg)) + 63.33
• 23C: 空気圧(psi) = (0.33 * 2.2 * 体重(kg)) + 53.33
• 25C: 空気圧(psi) = (0.33 * 2.2 * 体重(kg)) + 43.33
• 28C: 空気圧(psi) = (0.33 * 2.2 * 体重(kg)) + 33.33
• 32C: 空気圧(psi) = (0.17 * 2.2 * 体重(kg)) + 41.67
• 37C: 空気圧(psi) = (0.17 * 2.2 * 体重(kg)) + 26.67

上記計算は後輪のpsiである。前輪は後輪の空気圧に0.9をかける。衣類や、車重も本来考慮せねばなるまいが、厳密にはおおよそ上記式内に収まる。

まとめ：タイヤの最適解は25cなのか

タイヤは間違いなく25Cが主流になってきている。その理由は同一空気圧と同一体重であれば、タイヤの変形が少ないからだ。要素としては、同一空気圧であれば太いタイヤの方が転がり抵抗は小さい。しかしその分外周の外周が重くなる等のデメリットも有る。

外周の重さが増えれば重さの関係で加速が鈍くなるが、一度加速し巡航を考えれば25Cはアリな選択だ。ただ、「2bar空気を入れた60mm幅のタイヤ」と「4bar空気を入れた37mm幅のタイヤ」の「転がり抵抗」は互いに27.5Wattsであり、転がり抵抗の差はないように「どこに最適解」を持ってくるのかで答えは異なる。

したがって、現在のワールドツアーで25Cが主流なのはタイヤの変形による損失と空気圧の閾値から、23Cよりも変形が少ない（空力性能を考えたとしても）25Cが選ばれたのではないかと推測する。

タイヤの太さの特性上どこで「最適解が拮抗」するのかが重要である。25Cが使われる理由はデーター上「ある空気圧」において、23Cよりも25Cの方が「弾性損失」が少なく「転がり抵抗が小さい」と判断されたためと言える。

そう考えると転がり抵抗の90%は弾性損失ということからも、一度25Cを使ってその価値を試してみてはどうだろうか。