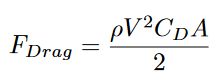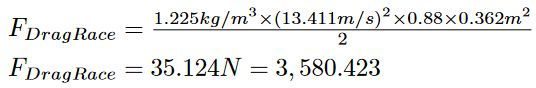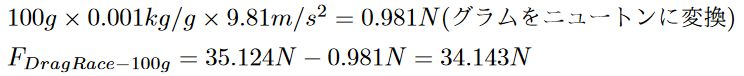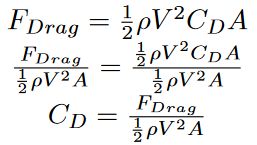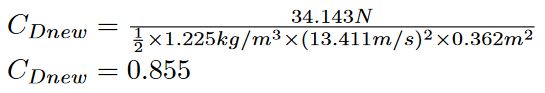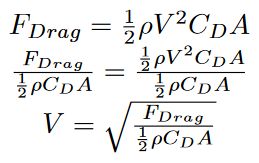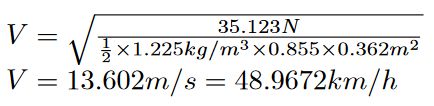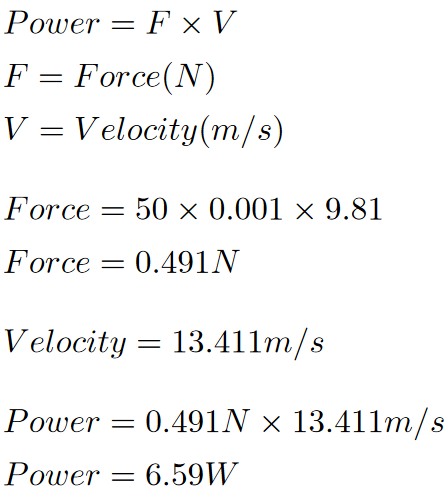ホイールの性能を語るとき、切っても切り離せないのがエアロダイナミクスだ。よく知られていることとしてはDragを減らすことでスピードは増し、タイムは短縮し、パワーセーブをしながら走れる。ホイールのエアロダイナミクス性能の重要性は十分すぎるほど理解されているが、わかっているようでわからない漠然とした疑問も数多くある。
例えば、次のような質問をされたらどのように答えれば良いのだろうか。
- CFDシミュレーションや風洞試験において48km/hを使用している。では、それ以下の遅い速度の場合でもエアロホイールの意味や効果はあるのか。
- 空気抵抗を50グラム減らすと、何ワットのパワーを節約できるのか。
1つめの質問に対する答えとしては、低速のほうがよりエアロダイナミクスの効果がある。直感とは反する逆の感覚・結果であるが、速度が遅いほどエアロホイールを用いてDragを減らすことでより多くのタイムを節約できる。
2つ目の質問に対する答えとしては、空気抵抗を50グラム減らすことは約6.5ワットのパワーセーブに相当する。例えば時速48km/hで走行している場合Dragを100グラム減らすと、40kmで40秒のタイムを短縮できる。
これらの数字や結果は、メーカーの風洞実験のデーターでしばしば登場しサイクリストの間ではよく知られている情報だ。しかし、私たちが走っている土地柄や環境条件を考えてみると、これらの数字はどれほど結びつくのだろうか。実際に、実世界との結びつきを理解するために役立っているとはあまり考えられない。
今回の記事は、Dragを減らすことでスピード、タイム、パワーにどのような影響を与えるのかを考察した。2021年1月下旬に実施予定の風洞実験前に、前提知識としてどのような要素がDragを決定し、ホイールの空力性能を決めているのか。計算式で確認しながらエアロダイナミクスに迫った。
相対速度
相対速度の話に入る前に抗力(以下、Drag)とは、物体の表面に働いてその運動を妨げる力のことだ。また、流体中を運動する物体に働く抵抗ともいう。もう一歩踏み込むと、流れの向きも考慮する必要があり、流れの速度に平行な方向で同じ向きの分力だ。また、流れの速度方向に垂直な成分は揚力(以下Lift)という。マイナス方向の揚力はよくお目にかかるダウンフォースと呼ばれている。
次に、風洞実験や計算を行う前に理解しておかねばならない重要な概念がある。それは相対速度だ。Dragを計算するとき、速度は単純に自転車で走行している速度ではない。自転車が走行している速度と風の速度を組み合わせを考慮する必要がある。この「自転車が進む速度」と「風の速度」の組み合わせを相対速度(Relative Velocity)という。
相対速度をイメージしやすいのは、自動車に乗っている時だ。
- 同一方向に走行する自動車A、Bがある。Aが40km/h、Bが70km/hで走行しているとき、Aの車内からはBが前方へ向けて30km/hで移動しているように”見える”。BからAを見た場合は、Aが後方へ向けて30km/hで移動しているように”相対的に見える”。
- A、B双方とも同じ速度で走行している場合、AからはBが静止しているように”相対的に見える”。(BからAを見た場合でも同様である。)
- AとBが対向しており、Aが40km/h、Bが70km/hで互いに接近しているとき、AからはBが前方より110km/hで接近してくるように”相対的に見える”。(BからAを見た場合でも同様である。)
5m/sの「追い風」の中を15msで走行していたとすると相対速度は10m/sになる(1番めのパターン)。5m/sの「向かい風」の中を15m/sで走行している場合、相対速度は20m/sになる(3番目のパターン)。
Dragは流体(空気や水)を介して物体の動きに抵抗する「力」ではあるものの、空気は目には見えないためDragの実感は湧きにくい。そこで同じ流体である水で埋め尽くされたプールを考えてみる。腰まで水深のあるプールに立って、一生懸命前に走ろうとすると水の抵抗を感じる。その時に感じる力がDragだ。とはいえ、空気は水ほどDragが大きいわけではない。
もしくは流れるプール(相対速度の関係にある)に逆らいながら、体を真っ直ぐに向けて進む場合と、体を横にしてカニさん歩きをするとでは、進む速度に差が生じる。どのような向きならばDragが小さくなるのかは、原理まではわからずともなんとなく頭と体で理解している。
これから数式がいくつか登場するが高校で学習するレベルの式だ。特段難しい式は登場しない。数式にはCloud LaTeXを使用した。ローカルにTeX環境を必要とせずクラウド上でコンパイルできる。便利な時代になったものだと感動したが、書き方は忘却の彼方へ忘れ去られていたので少々思い出すまでに時間がかかった。
そのため厳密に言えば表記方法、数式の表現、体裁は完璧ではないため、その辺りのツッコミはご容赦頂き、計算の概要がつかめればよしとする(以上を自身の最低条件とした)。
その上で、Dragを計算する場合は次の式を用いることで算出できる。
式の変数は以下のように定義されている。
Dragの式には2つの変数がある。
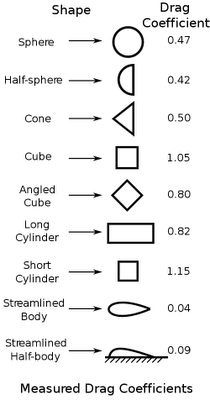
1つ目はDrag係数だ。Drag係数は形状に関係している。 Drag係数が小さいほどエアロダイナミクスが優れていることを示している。Drag係数は風洞試験で決定されている。ここでは、一般的な形状と関連するDrag係数のリストを以下に示す。
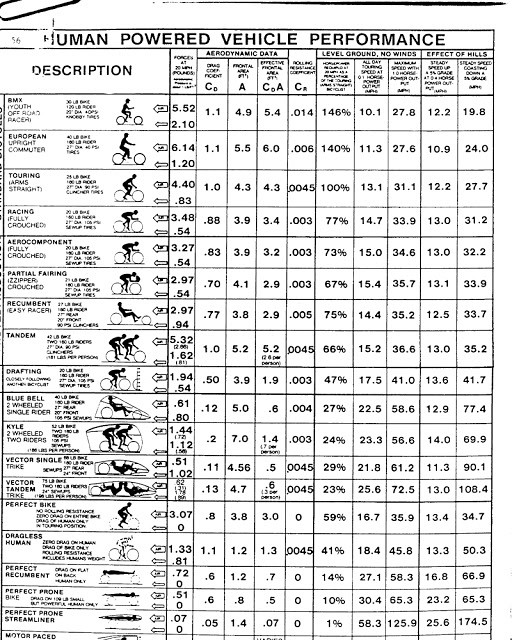
もちろん、Drag係数は上の図のような単純な形状に限定されるわけではない。どんな物体でもDrag係数を計算できる。 以下は、ライダーがバイクに乗車している状態のおおよそのDrag係数を示している。これから行う計算では4番目の「Racing(完全にしゃがんだ状態)」を採用する。
Cdが0.88、A(投影面積)が3.9ft^2だ。
A(投影面積)は一般的に「風が当たる部分」だ。たとえば、強い風の中に立っていることを想像してほしい。風に向かって立っていたとすると、風は体の前半分に接触する。体の後ろ半分と脇腹は風に直接触れることはない。このような状況では、体の前半分がA(投影面積)になる。
右に90度回転すると、体の左側が風を感じるようになり風と直接接触している領域になる。風洞実験で物体の角度(Yaw Angle)を0~20°変更するのも同じだ。風を受ける角度の変化で投影面積は変動し空力性能に影響を及ぼす。今回の計算では上の表の3.9ft^2(0.362m^2)の値を使用する。
Yaw Angleの研究で参考にした論文は、「A New Method for Analysing the Effect of Environmental Wind on Real World Aerodynamic Performance in Cycling (自転車ホイールのヨー角分布の数学モデル)」(ZachMcCormick、Nick McCormick、Justin Clarck)だ。現実世界でライダーが遭遇する風向きのほとんどが0~10°であり、10~20°または20~30°の風向きが発生することは実はそれほど多くはない。
FFWDのRYOT55の風洞実験データーが10°までしか掲載されておらず、「都合のいい部分だけ切り取ったな」と勘ぐっていたが、論文にもあるとおり実世界で発生する風向きのほとんどが10°以下だった。
実際にレースコースを走った実験でも同様の結果が得られている。風速計をバイクに搭載しハワイ州コナで開催されたIronMan世界選手権を走行した実験では、72.1%が10°未満のYaw Angleだった。そのため、実際の風洞実験の結果から計算を行う際には加重平均計算を用いる(0°が最も重み付けされる)。本記事内では触れないが別の記事として掲載予定だ。
40kmで40秒短縮
時速48kmで走行している場合100gのDragを減らすことで、40kmのタイムトライアルで40秒ほどタイムを短縮できるとされている。これが事実であることを確認するために、上の表のCdと投影面積を用いてサイクリストが経験するDragを計算する。
まず、式に用いる数値を示す。補足事項として、(Drace)といったタグは異なる値を識別するためだけに使用している。計算式が進むにつれて複数のCd値を使用するため、それらを識別するための方法として用いた。
これらの値を使用し、”Racing(完全にしゃがむ)”の位置でサイクリストが経験するDragを計算した。
計算結果は相対速度48km/hで走行した場合、平均3,580.423gのDragが発生することがわかる。
次に、Dragの値を100g減らした場合どのような結果が得られるか確認した。
新しいDragの値が算出できたので、Dragの方程式を再配置して新しいCd値を計算する。よく知られている事として、Dragを減らためには前方投影面積Cdの値も減る必要がある。これは計算式からも読み取れる。
新しい式を用いると、Dragが100g減少したときの新しいCd値を算出できる。
Dragを100g減らすことで得られた新しいCd = 0.855を用いて、Dragの式を再度組み立て直す。この例では、元のDragと新しいCd値を用いて新しい速度を計算しなおした。
(注: 速度が増加するとDragも増加する。よって、厳密な計算であるとは言い難い。そのため、非常に近しい推定値を算出している。正確な数値を知るには今後予定している風洞実験などで実際に確認する必要がある。)
これで新しい速度を計算できる。この計算式からどのような値が得られるか確認する。
新しい速度が得られたので、40kmのレースでタイムをどれくらい削減できるかを算出できる。
以上の計算から48km/hで走行している条件でDragを100g減らすと、40kmで約40秒のタイム削減になることがわかった。1.95秒の差については、前方投影面積の違いやCdの値の違い、速度の上昇がDragの値に与える影響等を厳密に考慮していくと0に近づいていくと考えられる。
上記の計算が便利なのは、ある速度においてどれ程タイムを節約できるか簡単に計算できる点だ。Cd値は物体が移動している間、どのような速度域であっても関係なく絶対的なCd値であり、計算の全てにおいて一定である。
次に50グラムのDrag低減で、48km/hで6.5ワットのパワーセーブという条件を考える。風洞実験結果で頻繁に登場する内容で、機材と機材の比較で用いられる。この計算はこれまでと比べて簡単だ。方程式を確認する。
差分は0.59Wほど生じるが、おおよそ「50グラムのDrag低減で、48km/hで6.5ワットのパワーセーブ」という基準が正しいことを証明している。
まとめ:計算式から風洞実験へ
風洞実験を実施する前に基本的な知識として、48km/hでのパワーセーブという条件における基礎的な計算を行った。恥ずかしながら、まったくの無知からやっとスタートラインに立てただけに過ぎない。高校の物理範囲だ。他にも考慮すべきこと、冒頭の論文で触れたとおりYaw angleの違いによる加重平均の計算など取り入れるべきことは多い。
今回の記事はエアロダイナミクスの重要性、バイクを進ませるために必要な時間、DragやCdAといったものがどのように影響するかを理解するために用いる。次回は1月下旬に風洞実験室で実際にホイールテストを行う模様をお伝えする。


¥3,080